Stalo se pod blíže neurčenými Suchými skalami nedaleko Malé Skály v severních Čechách. Paní Rž (učitelka matematiky), pan Jan s panem PH a známý pes Dagles odpočívali u cesty pod skalami, paní Rž nad cestou, pánové a pes o kus dál pod cestou. Paní Rž podřimovala, když tu v polospánku zaslechla varovné: Hele pes! Otevřela levé oko (na to lépe vidí), pak i pravé a mohutným skokem se vrhla na Daglese, který volným klusem běžel kolem ní vstříc psímu vetřelci, aby mu, jak bylo jeho zvykem, trochu načechral kožich a řekl, co si o něm myslí. Ale již byl držen paní Rž za ocas a tažen zpět. Zpěčoval se, hrabal nohama, snažil se vymanit ze sevření, aniž se odvážil ohnat. Paní Rž nepovolila, ale ani Dagles a stále se tvrdošíjně dral dopředu. Tady něco nehraje, blesklo hlavou paní Rž. Zvedla oči od psího ocasu... proti ní žádný pes, jen dvojice, v bezmocném úžasu sledující, jak se jakási divoženka snaží odvleci jejich krásného německého ovčáka. Z dálky vše v klidu sledoval Dagles, říkaje si, že do tohohle se paničce plést nebude. Ruce paní Rž klesly a k smrti vyděšený Daglesův dvojník uháněl schovat se před tou líticí za své páníčky.
Letos uplynulo 20 let od smrti Richarda Feynmana (11. 5. 1918 - 15. 2. 1988, Nobelova cena za fyziku 1965), významné a velmi výrazné postavy vědy 20. století.
Feynman nesmírně miloval fyziku (zároveň však říkal, že bez znalosti patřičného matematického aparátu nelze fyzice dobře porozumět), ale fyzika nebyla jediná. Byl ohromně zvědavý a zajímal se o všechno možné. Neváhal lézt po čtyřech po koberci, aby zjistil, zda může v čichových schopnostech soutěžit se psem. Prohrál. Zjišťoval, zda může vědomě ovlivňovat své sny - mohl. Hrál na bonga (prý dobře). Když učil fyziku v Riu v Brazílii, uplatnil své bubnování na věhlasném karnevalu. Řešil i drobné záhady a otázky běžného života. Např. proč se čajové lístky nebo smítka v hrnečku shromažďují při míchání uprostřed. Nebo se hádal s kamarády, jestli moč z těla vychází jen gravitací. přesvědčil je experimentem. Ukázal jim, že může močit i stoje na hlavě.
Při návštěvě cizí země míval ve zvyku naučit se trochu jazyk. S portugalštinou neměl problém, ale u Japonštiny narazil. Když se učil slovo dívat se, zjistil ke svému zděšení, že záleží na tom, kdo se na co dívá. Ve větě: Smím se podívat na vaši zahradu? se musí použít zdvořilejší tvar, než ve větě: Nechcete se podívat na mou zahradu?. Vlastně říkáte: Nechcete se kouknout na mou ubohou zahradu?, zatímco v prvním případě: Smím spatřit vaši nádhernou zahradu?. Jdete-li však do kláštera, kde mají opravdu nádhernou zahradu, musíte zvolit ještě zdvořilejší tvar, aby to vyznělo: Smím spočinout zrakem na vaší přenádherné zahradě?. To už Feynmanovi šla hlava kolem, ale dělal si naděje, že ve vědecké konverzaci je vše jednodušší. Mýlil se. Byl ubezpečen, že jiné řešit se použije, řeší-li Diracovu rovnici on a jiné, řeší-li ji někdo jiný. Tím pro něj výuka japonštiny skončila.
Jednou z jeho velkých zábav bylo otvírat sejfy. V Los Alamos (středisko v Nevadské poušti, kde se pracovalo na vývoji atomové pumy) se mu podařilo dostat se do hlavního trezoru - otevřel jej, nechal vzkaz a zase zavřel. Druhý den ráno šéf projektu Oppenheimer nevěřil svým očím.
Feynman se velmi zajímal i o věci veřejné. Zasloužil se o objasnění příčin havárie raketoplánu Challenger v roce 1986.
Je toho spousta, co by se dalo ještě napsat. Mnohé najdete v jeho knihách.
S geometrickou řadou se setkáme leckde. Díky ní Achilles hravě dohoní želvu (ve Starém Řecku řady neznaje s tím měl velké potíže), na účtech nám naskakují úroky a pan Helge von Koch nás zasypává svými vločkami. Více se dočtete zde.

Následující se mohlo stát kterémukoliv z nich. Jedna z poslucháren na Karlově (nebo jich bylo víc?) měla dvoje dveře - taková malá past. I stalo se: pan profesor vešel do posluchárny plné vědychtivých studentů a seznav, že křídy se nedostává, omlouval se: „Chvilinku strpení, prosím, dojdu pro křídu,“ a opustil posluchárnu nejbližšími dveřmi. Vzápětí se objevil v druhých dveřích: „Nemáte prosím přebytečnou křídu?“ Studenti ho zdvořile ujistili, že nemají vůbec žádnou křídu, a pan profesor se vrátil. „Vedle taky nemají křídu,“ a jal se přednášet bez křídy.
Italský fyzik Enrico Fermi (1901 - 1954) byl jako jeden z mála nejen excelentní experimentátor ale i teoretik. Uměl si pokus připravit, provést jej a zároveň si spočítat, co by se asi mělo naměřit. V pohnuté době čtyřicátých let minulého století se nechal „zavřít“ v Los Alamos v USA, aby zde spolu s dalšími významnými vědci té doby pracoval na vývoji atomové bomby. Bylo třeba předhonit Němce. Ale o tom teď nebude řeč. V Los Alamos žili někteří vědci i se svými rodinami - stejně tak Fermi. Jeho ženě, zvyklé na slunnou Itálii, bylo však v jejich bytě zima a rozhodla se, že nechá zdvojit skla v oknech, aby měli tepleji. Jako správná manželka to konzultovala s manželem. Fermi vzal tužku a papír, chvíli počítal, a pak řekl, že je to zbytečná investice, neboť účinek by byl nepatrný. Paní Fermi, jako správná manželka neodporovala, pokývala hlavou…a dala udělat dvojitá skla do oken. Účinek byl víc než patrný. Fermi se nerozzlobil, že jeho výpočty nebyly brány vážně, ale znovu se chopil tužky a papíru. Ve výpočtech byl řádová chyba.
Lidé mívají s matematikou někdy problémy. Někdy bývají problémy i se samotnými matematiky.
Slyšte:
Matematik Norbert Wiener byl znám svou roztržitostí. Stalo se , že se s rodinou přestěhovali, čehož si Wiener tak trochu nevšiml. Došel tedy na starou adresu a zjistil, že tam bydlí někdo jiný. Před domem uviděl stát chlapečka a ptá se ho: „Nevíš, kam se přestěhovali Wienerovi“? „Neboj tati , už na tebe doma čekáme. Maminka říkala, abych tě přivedl.“
S matematiky může být někdy docela zábava. Zábavná ovšem může být i samotná matematika.
Jedna ze základních dovedností matematika je umět převést daný problém na problém již vyřešený. V reálu to může vypadat například takhle:
Matematika naučili vařit čaj: vezmeš prázdnou konvici, naliješ do ní vodu,dáš vařit a vroucí vodou zaliješ připravený čaj.
Ale co když se pak matematik dostane do situace, kdy má konvici již plnou vařící vody? Ví si rady. Vylije vodu a problém je převeden na známý případ.
Pythagoras (6.st. před Kristem) založil společenství -- Pythagorovo Bratrstvo, jehož členové museli přísahat, že nikdy ne
vyzradí nikomu mimo Bratrstvo žádný z matematických objevů Bratrstvem dosažených.
Mnoho lidí by rádo do Bratrstva proniklo, přijati byli však jen ti nejlepší. Tak se mezi odmítnutými objevil i muž jménem
Kylon. Odmítnutí ho velmi urazilo a byl rozhodnut se pomstít. Na "svůj" okamžik dokázal čekat dlouhých 20 let.
Při nepokojích v Krotonu, kde Pythagoras se svou věhlasnou školou sídlil, se Kylonovi podařilo navést zfanatizovaný dav k
e zničení Pythagorovy školy. Dav obklíčil školu, zatarasil východy a vše zapálil. V plamenech našlo svůj konec mnoho Pythagorových žáků i sám Pythagoras.
Uražená lidská ješitnost tak zničila jednu z nejlepších škol starověku i s jejím zakladatelem velkým matematikem a filosofem.
Leonhard Euler, věhlasný evropský matematik 18. století, působil
dlouhá léta na dvoře ruské carevny Kateřiny Veliké.
Ve stejné době na dvoře pobýval i slavný francouzský encyklopedista
Denis Diderot, který zde s velkým zápalem šířil svůj ateistický názor.
Kateřinu Velikou to velmi hněvalo i požádala Eulera, aby tomu učinil přítrž.
Euler slíbil, že to zařídí, neboť má algebraický důkaz existence Boha.
Kateřina Veliká tedy pozvala oba muže do svého paláce na filosofické klání a
sezvala rovněž početné dvořanstvo. První předstoupil před shromážděné
posluchače, kteří napjatě čekali, co bude, Euler a začal disputaci:
„pane,
a proto Bůh existuje. Co odpovíte?“ Jenže Denis Diderot měl ke své smůle nulové znalosti algebry a tento výpad nedokázal odrazit. S hanbou opustil Petrohrad a vrátil se do Paříže.
Vypráví se o matematiku Norbertu Wienerovi.
Wienerovi se měli stěhovat z jednoho konce Cambridge na druhý. Paní Wienerová dobře znala svého manžela a věděla o jeho roztržitosti, a tak se rozhodla připravit ho na celou akci předem. Měsíc před stěhováním říká ráno manželovi před jeho odchodem na fakultu: “Norberte, ode dneška za třicet dnů se stěhujeme. Až pak půjdeš ze školy, nenastupuj do autobusu 33, ale musíš do autobusu 14!“ Wiener odvětil: “Ano, drahá.“ Druhý den ráno paní Wienerová zase povídá: “Norberte, pamatuj si, za devětadvacet dnů se stěhujeme. Až pak půjdeš ze školy, nenastupuj do 33ky, ale do autobusu 14!“ Wiener odvětil: “Samozřejmě, drahoušku.“ A tak to šlo den co den, až do dne, kdy mělo vypuknout stěhování. Paní Wienerová ráno povídá: “Tak Norberte, nezapomeň, dneska se stěhujeme! Až dnes půjdeš ze školy, ne abys nastoupil do autobusu 33, jeď 14tkou!“ “Ano drahá,“ odvětil Wiener a pustil to z hlavy. Nu a když odcházel z fakulty, samozřejmě nastoupil do autobusu 33, dojel domů, a hleďme - byt prázdný. Vzpomněl si: No ovšem! Dneska jsme se přece stěhovali! Vrátil se tedy k univerzitě, nasedl do 14tky a vystoupil na stanici, o níž si pamatoval, že je to ta jejich. Jenomže zapomněl, kde teď bydlí. Bloudil kolem dokola, až se setmělo. Nakonec zastavil nějakou dívku a zeptal se jí: “Prosím vás, nevíte náhodou, kde tu teď bydlí Wienerovi?“ Dívka odpověděla: “Samozřejmě tati, dovedu Tě domů.“
Stalo se v Rusku za občanské války. Všichni tenkrát bojovali se všemi, do toho tyfus, hlad a Leninův NEP (nový ekonomický program) a zase hlad.
Tehdy se muž jménem Igor Jevgeňjevič Tamm (nositel Nobelovy ceny za fyziku v roce 1958) vydal z Oděsy do blízké vesnice, aby se pokusil vyměnit půltuctu stříbrných lžic za něco k jídlu. Zatímco vyjednával s jedním vesničanem, obsadila vesnici skupina Machnovců, která pronásledovala rudé. Tamm se jim zdál velmi podezřelý. Zajali ho a předvedli před atamana. Vysoký fousatý muž, hruď ozdobená pásy nábojů do kulometu, za pasem pár ručních granátů, se vůbec netvářil přátelsky. Nastínil Tammovi, co s ním jako s bolševikem udělají.
Tamm se bránil: "Jsem profesorem matematiky na univerzitě v Oděse, tady jsem jen sháněl něco k jídlu."
"Cože to učíš?"
"Matematiku."
"Dobře, tak mi tedy pověz, jaký je odhad chyby, kterou uděláme, když ukončíme Maclaurinovu řadu n-tým členem. Jestli to dokážeš, můžeš běžet. Jestli ne, budeš zastřelen."
Tamm nevěřil svým uším. Maclaurinovy řady by se na těchto místech nenadál. Třesoucí se rukou pod hlavní pušky napsal řešení a podal ho atamanovi.
"Správně. Vidím, že's nelhal. Jsi volný."
Kdo byl ten muž a kde a jak skončil, se Tamm nikdy nedověděl. Možná se taky stal profesorem matematiky.
Ve středu 30. května 1832 nad ránem byl v souboji s vyhlášeným střelcem d´Herbinvillem postřelen do žaludku a ponechán svému osudu nadějný francouzský matematik Evariste Galois. (Důvod souboje -- jak jinak -- žena… nebo možná politika, historici se nemůžou dohodnout.) Galois neměl sekundanta a o souboji nikomu předem neřekl, jen poslal zprávu svému bratru Alfredovi. Zpráva však došla pozdě a Alfred našel bratra až po několika hodinách, kdy už mu nebylo pomoci. Druhého dne mladý matematik v nemocnici umírá.
Evariste Galois se narodil 25. října 1811. Své zájmy brzy začal dělit mezi matematiku, ve které projevoval nebývalé nadání, a politiku, která mu působila četné problémy. Již v šestnácti letech byl schopen vstřebat nejnovější matematické poznatky své doby, v sedmnácti publikoval svůj první matematický článek, ve dvaceti byl na několik měsíců uvězněn za údajné usilování o králův život. Byl poněkud prudký a ukvapený jak v matematice, tak v politice.
Při vysvětlování řešení matematických problémů prováděl spoustu výpočtů zpaměti a příliš se neobtěžoval své myšlenkové pochody podrobněji objasnit, čímž nesmírně popouzel své učitele, kteří ho nestačili sledovat.
Díky této neochotě trochu podrobněji věc vysvětlit, neudělal ústní zkoušku na prestižní Ecole Polytechnique, po které velmi toužil. Zkoušel to ještě další rok, ale při ústní zkoušce opět nedokázal než být příliš stručný. Zkoušející mu nerozuměl a zoufalý Galois cítě, že zas neuspěje, ve vzteku mrštil po examinátorovi houbou -- a trefil… Ecole Polytechnique pro něj zůstala navždy uzavřena.
To ho však neodradilo, aby se dál nevěnoval své milované matematice. Fascinovalo ho hledání řešení algebraických rovnic. V 19. století byly již známy návody, jak řešit algebraické rovnice 2. 3. a 4. stupně a Galois toužil najít postup k řešení rovnic 5. stupně. Ale pletly se mu do toho politické události (ve Francii té doby bylo velmi živo) a nakonec přišel souboj s vyhlášeným střelcem. Galois věděl, že v souboji nemá naději, a strávil noc před soubojem sepisováním svých poznatků týkajících se řešení rovnic 5. stupně. V časové tísni a ze zvyku ale své myšlenky příliš nevysvětloval, a tak se stalo, že jeho poznámky málem upadly v zapomnění. Až v roce 1846 se Joseph Liouville prokousal Galoisovými zápisky a publikoval je ve svém časopise. Bylo jasné, že Galoisovi se podařilo podat vysvětlení, jak postupovat při řešení algebraických rovnic 5. stupně.
Poznámka: Tuto Galoisovu práci použil Andrew Wiles při dokazování Velké Fermatovy věty.
To takhle jednou obě skupiny studentů jely na nějakou akci vlakem. Právníci si koupili hromadnou jízdenku a radovali se, jak ušetří. Matfyzáci šetřili ještě víc -- koupili si jeden lístek dohromady.
Právníci si mezi sebou šuškali: „Tedy ti matfyzáci dělají všeljaké skopičiny, ale tohle už jim fakt projít nemůže! To jsme zvědaví, co budou dělat, až přijde průvodčí…“
Když se blížil průvodčí, matfyzáci jako jeden muž napochodovali na záchod. Průvodčí zkontroloval právníky, ti se potutelně usmívali a ukázali průvodčímu směrem ke dveřím… „ale na záchodě…“
Průvodčí tedy „buch buch buch“, zaklepe na záchod, otevřou se dveře, vysune se ruka s lístkem. Průvodčí si vezme lístek, štípne ho, vrátí a jde dál. Právníci jsou zklamaní, ale říkají si: „To je dobré, příště to uděláme taky tak.“
Pak se jede z akce zase zpátky. Právníci si koupí všichni dohromady jeden lístek, matfyzáci se ale opili, rozprchli, zmizeli… no zkrátka domů jel jenom jeden a ten si pro jistotu nekoupil žádný lístek.
Právníci se ujišťují, že tohle už musí prasknout a těší se na tu legraci. Když se blíží průvodčí, zalezou všichni na záchod. Ke dveřím přijde matfyzák „buch buch buch“, zpoza dveří se vysune ruka, matfyzák si vezme lístek, popoběhne a ukáže ho průvodčímu. Štípnutý lístek vrátí za dveře, znovu doběhne za průvodčím… „ale na záchodě!“
A od té doby se nemají právníci s matfyzáky rádi…
S laskavým svolením převzato od Aničky Bernáthové.
Jestliže rozdělíme úsečku na dvě části tak, že poměr délky celé úsečky ku delší části je stejný jako poměr delší části ku kratší, pak jsme ji rozdělili tzv. zlatým řezem. Uvedený poměr je 2/(√5-1)≈1,618.
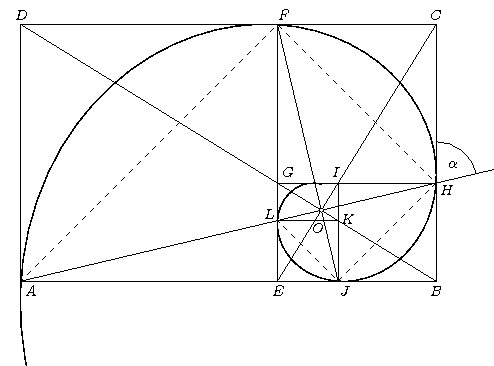
Logaritmická spirála je křivka, která je v polárních souřadnicích r, φ popsána rovnicí lnr=kφ, kde k je reálná konstanta různá od nuly.
A jak spolu souvisí zlatý řez a logaritmická spirála? Takhle: vyjdeme ze „zlatého obdélníku“ ABCD (strany jsou v poměru zlatého řezu) a do něj postupně vpisujeme otáčející se menší a menší obdélníky. Každý další je vůči předchozímu otočen o π/2 a zmenšen v poměru zlatého řezu. Bod A se otočí kolem bodu E do bodu F, bod F otočíme kolem G do H,… Body E, G, I,… dělí příslušnou stranu v poměru zlatého řezu, body A, F, H, J,… jsou body logaritmické spirály. Přibližný průběh spirály je dán drahami otáčejících se vrcholů, tj. čtvrtkružnicemi, které mají středy ve středech otáčení. Pól spirály (na obrázku bod O) je průsečík např. BD a EC.
Logaritmická spirála má jednu úžasnou vlastnost: všechny polopřímky vycházející z pólu ji protnou pod stejným úhlem. K čemu se to může hodit? Využívá toho např. sokol stěhovavý, který údajně nalétává rychlostí až 300 km/hod na kořist po logaritmické spirále, přičemž kořist je v pólu spirály. Zmíněná vlastnost spirály sokolu umožňuje během letu nepřetržitě sledovat kořist, aniž by musel stáčet hlavu a tím případně zpomalit let. Kdyby letěl po přímce, pohybům hlavy by se díky umístění očí nevyhnul a kořist by měla větší naději na útěk.
Vypráví se o matematiku Norbertu Wienerovi.
Wienerovi se měli stěhovat z jednoho konce Cambridge na druhý. Paní Wienerová dobře znala svého manžela a věděla o jeho roztržitosti, a tak se rozhodla připravit ho na celou akci předem. Měsíc před stěhováním říká ráno manželovi před jeho odchodem na fakultu: “Norberte, ode dneška za třicet dnů se stěhujeme. Až pak půjdeš ze školy, nenastupuj do autobusu 33, ale musíš do autobusu 14!“ Wiener odvětil: “Ano, drahá.“ Druhý den ráno paní Wienerová zase povídá: “Norberte, pamatuj si, za devětadvacet dnů se stěhujeme. Až pak půjdeš ze školy, nenastupuj do 33ky, ale do autobusu 14!“ Wiener odvětil: “Samozřejmě, drahoušku.“ A tak to šlo den co den, až do dne, kdy mělo vypuknout stěhování. Paní Wienerová ráno povídá: “Tak Norberte, nezapomeň, dneska se stěhujeme! Až dnes půjdeš ze školy, ne abys nastoupil do autobusu 33, jeď 14tkou!“ “Ano drahá,“ odvětil Wiener a pustil to z hlavy. Nu a když odcházel z fakulty, samozřejmě nastoupil do autobusu 33, dojel domů, a hleďme - byt prázdný. Vzpomněl si: No ovšem! Dneska jsme se přece stěhovali! Vrátil se tedy k univerzitě, nasedl do 14tky a vystoupil na stanici, o níž si pamatoval, že je to ta jejich. Jenomže zapomněl, kde teď bydlí. Bloudil kolem dokola, až se setmělo. Nakonec zastavil nějakou dívku a zeptal se jí: “Prosím vás, nevíte náhodou, kde tu teď bydlí Wienerovi?“ Dívka odpověděla: “Samozřejmě tati, dovedu Tě domů.“
Stalo se na universitě v Kodani. Konala se zkouška z fyziky a otázka zněla: “Popište, jak určit výšku mrakodrapu pomocí barometru.“
Zkoušený student bryskně odpověděl: “Upevníte dlouhý kus provazu k vrchu barometru, pak spustíte barometr se střechy mrakodrapu na zem. Délka provazu plus výška barometru se rovná výšce budovy.“
Tato vysoce originální odpověď rozzuřila zkoušejícího natolik, že studenta vyhodil. Student se odvolal s tím, že jeho odpověď byla nepochybně správná, a univerzita jmenovala nezávislého arbitra, aby případ rozhodl.
Arbitr usoudil, že odpověď byla opravdu správná, ale neukázala žádné zjevné znalosti fyziky. K vyřešení problému bylo rozhodnuto zavolat studenta a dát mu šest minut, během kterých by měl ve slovních odpovědích prokázat alespoň minimální obeznámenost se základními principy fyziky. Student seděl tiše, čelo svraštělé přemýšlením. Po šesti minutách mu arbitr připomněl, že čas už vypršel. Student odpověděl, že má několik velmi závažných odpovědí, ale nemůže se rozhodnout, kterou zvolit. Arbitr jej, už poněkud netrpělivě, vyzval, aby konečně spustil. Dostalo se mu takovýchto odpovědí:
“Zaprvé můžete vzít barometr na střechu mrakodrapu, hodit ho přes okraj dolů a měřit čas, než barometr dopadne na zem. Výšku budovy lze spočítat podle vzorce h = ½gt². Pro barometr to ale bude smůla.“
“Nebo, pokud svítí slunce, můžete změřit výšku barometru, pak ho postavit na zem a měřit délku jeho stínu. Pak změříte délku stínu mrakodrapu a potom je jednoduchou záležitostí pomocí poměrné aritmetiky spočítat výšku mrakodrapu.“
“Pokud byste ovšem chtěli být vysoce vědečtí, mohli byste upevnit krátký kus provázku k barometru a zhoupnout jím jako kyvadlem, nejdřív k zemi a pak ke střeše mrakodrapu. Výška se vypočítá z rozdílu v gravitační síle. “
“Nebo pokud má mrakodrap venku únikové schodiště, bylo by jednodušší vyjít nahoru a označovat celou výšku budovy pomocí délky barometru a pak to sečíst.“
“Kdybyste ale chtěli být jenom nudní a ortodoxní, pak byste mohli použít barometr k měření tlaku vzduchu nejdřív na střeše mrakodrapu a pak u země, potom převést rozdíl tlaků v milibarech na stopy, a dostali byste tak výšku budovy.“
“Protože jsme ale trvale nabádáni, abychom uplatňovali nezávislé myšlení a používali vědecké metody, bylo by nepochybně nejlepší zaklepat na domovníkovy dveře a říct mu: Kdybyste chtěl pěkný nový barometr, dal bych vám tenhle, když mi sdělíte výšku tohoto mrakodrapu.“
Kdo byl ten student? Niels Bohr, jediný člověk z Dánska, který získal Nobelovu cenu za fyziku.Matematička na pískách
(aneb trocha poezie nikoho nezabije)
Vzhůru na cenoman ano byl to on
co u Turnova leží slavný Panteon
já a moje žena a k tomu též
slovutný horolezec tenhle Václav Š.Na Trollryggenu a dalších stěnách on se pochlapil
aby bylo jasno on to teda byl
už stojíme pod čímsi převislým a bez chytů
a Širl hnedle volá Cesta vede tuUž se sápe funí kleje dosahuje kruh
my voláme uchváceni Lezeš jako Bůh!
moje žena plavným stylem vzhůru za ním pílí
když tu ouha znenadání ji opouštějí sílyVolá Václav hola tohle se nezmění
spěchej vzhůru milý Jene to chce saské stavění
vyrazil jsem tedy směle nějak to překlepal
ufuněný vykulený pak jsem u ní stálDo spárky dal uzlík a lehce odsedl
že nevypadne to jsem věřil jak jen jsem dovedl
potěchou mi bylo míti ženu milenou
postavenou přímo na mých mužných ramenouKdyž však stála na mé hlavě k tomu na špičkách
o výsledek téhle akce počal jsem mít strach
leč chytla chyt a jako kočka skáče po kruhu
a po chvíli i já šťastně sedím u druhůVšak víme až na vrcholu cesta má svůj konec
proto Václav opět v akci věru je to borec
co však dělá tázal jsem se za děsné koniny
proč na hlavu nám hází kýble zeminyZešílel to je jasné či se začal bát?
vzpomenuv vojenských let chce se zakopat?
možná také správně věc tu zhodnotil
maká maká maká -- by hrob si zhotovil.Pak lezla žena -- a tohleto mi věř
kolem hlavy prolétl mi každou chvíli keř
když řada přišla na mne trochu jsem se bál
bylo to mnohem horší ten hliněný val.Však po bolu na vrcholu sešli jsme se zase
jeden každý spokojený a špinavý jak prase
turisté tu na prohlídce nás filmovali hlavně
Dlouho jsem se necítil se teda takhle slavně.